The algorithm has been developed in the DSP. In order to do that, the two communication channels from Gc to DSP has been used to send the power and the demodulated signal (position error signal) acquired by the photodiode in transmission at the end of the north cavity. In the following plots, Sc_NE_pow is equivalent to Pr_B7_DC, and Sc_NE_sig is equivalent to Pr_B7_ACp/Pr_B7_DC (the normalization increase the linear range of the error signal).
As a first step, a pure derivative damping has been implemented and tested.
The velocity signal is computed by filtering the position error signal by a zero@0 and a pole@200Hz.
A force proportional to the velocity is sent in feedback to the RM coils.
The computation of the velocity is limited to the crossing time of the resonance (a trigger on the power is used); out of resonance, the signal does not make sense, and v is kept as a constant at its latest computed value.
The force starts to be applied when the
The application period of the force is limited too, but the window is larger (the triggerOut is very low).
The available force is limited to a value which is about 300 times lower than the maximun provided by the present actuation setup. In this way we want to test the possibility to use smaller magnets for Advaced VIRGO mirrors.
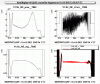
In figure 1 we see a successful locking attempt: the cavity stays close to the resonance for 2 seconds, while the loop keeps the velocity at zero. The position signal is expressed in microns, the velocity in um/s, the correction in uN.
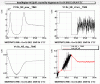
In fig 2 a zoom of the first instant of the lock acquisition is shown. When the action is triggered, the requested force exceeds the limit, and it is kept constant during the first crossing of the resonance. But this force is enough to reverse the motion, and the resonance is crossed again with a lower speed. A second full-dynamic action is applied in the opposite direction for a while, then the signal enters the linear regime and the loop is closed.
to be continued...