ITF found in Commissioning mode; activity concluded at 15:50 UTC and ITF set in Science mode.
At 16:14 UTC we had a period of missing data:; Hrec went to zero but the ITF kept the lock. I was able to find the following error message on SUSP_Fb: 2025-07-18 16h14m48 UTC [TolmFrameBuilder::FrontEnd] Rtai DAQ FIFO overrun -> acquisition is reset .
Guard tours (time in UTC)
18:00-18:40
On request of Michal, the SDB2_B1p_QD1_{H,V}_norm channels are now sent to rtpc1 to be available for the SDB1_LC server :
The SDB1_LC server configuration has been updated by adding as commented part the readout of the SDB2_B1p_QD1_{H,V}_norm channels
Today, I found ITF in SCIENCE. 9:28 UTC ITF status in COMMISSIONING for working on a fine tuning of the locking acquisition (ISC crew, M. Was, I. Nardecchia).
Sub-system reportsDAQ
12:48 UTC A. Masserot SDB2 quadrants process stopped and restarted.
We noticed that the CEB acoustic injection was not performed during the last automated injections. The colored noise was correctly sent to the DAC, but the loudspeaker did not emit any sound (see Fig. 1).
The issue was traced back to the PDU: the loudspeaker was not powered on during the injection. We found the VPM process Loudspeaker_PDU in grey status, and even after a reload, its status remained unchanged.
To fix the issue, we switched off and unplugged the PDU in the CEB DET terrace. After reconnecting, the process turned green again (see Fig 2). We then tested the system by injecting a 300 Hz line and the loudspeaker is now working properly.
We tried to solve the lock acquisition issues by tuning the CH powers.
The nominal starting values are listed below.
|
| Reference | CH [W] | INNER DAS [W] | OUTER DAS [W] |
|---|---|---|---|---|
| W | on the ITF | 0.048 | 0.150 | 1.79 |
| on the pickoff | 0.297 | 0.025 | 0.291 | |
| N | on the ITF | 0.105 | 0.340 | 3.1 |
| on the pickoff | 0.648 | 0.052 | 0.502 |
I manually unlocked the ITF at 13:29 UTC and set it to CITF.
The steps taken are summarized below:
At 13:47 UTC in CITF, the NI CH power was decreased by 10%:
Initial value: 0.648 W
New value: 0.648 × (1 – 0.10) = 0.583 W
→ Negative impact on sidebands and fringe; two lock acquisitions failed
At 14:48 UTC in CITF, the NI CH power was increased by 20% with respect to Step 1:
→ ITF unlocked twice
The WI CH has been increased by 10 mW (48 mW → 58 mW)
→ ITF unlock
The WI CH has been increased by further 10 mW (58 mW → 68 mW)
→ ITF unlock
Despite the various changes, the interferometer still unlocks in the same way.
In agreement with the control room, I kept the values from the last step.
A comparison of B1p, B4_DC, B4_12 MHz, and B4_112 MHz using the initial CH power values and the updated ones — corresponding to step 4 for WI and step 2 for NI — is shown in the attached figure.
All quantities increased coherently by approximately 7%.
Yesterday evening the successful lock acquisition was achieved by misaligning SR TY by ~2urad in DRMI before continuing the lock acquisition. This is in fact the standard lock procedure during the science run as SR TY is misaligned by 2urad in LN3, and SR is not realigned in DRMI. It only gets realigned in CARM NULL 1F, and the misaligned again at the LN2->LN3 transition.
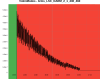
Figure 1 shows a standard lock acquisition last week when there was lots of unlocks from LN3 caused by BS F0 glitches. SR TY is at -221 at the beginning, then comes back to that position after the unlock (where SR is misaligned to remove it from the CITF), the ones the interferometer reaches CARM NULL 1F SR TY progressively decreases to -223, and then finally at ~19:30 UTC it increases back to -221 during the LN2->LN3 transition
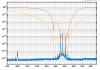
Figure 2 shows the successful lock acquisition of last night, it reproduces the same shaep of SR TY alignment. However the misalignment had to be done manually, using many manual steps of SR TY.
Figure 3 shows a normal lock acqusition, the SR TY DCP HF B1p I signal is away from zero and the moves to zero as SR TY moves from -221 to -223 in CARM NULL 1F. If I am not mistaken that is the error signal for the SR TY loop in CARM NULL 1F.
Figure 4 shows the same last night. There is no changes on SR TY DCP HF B1p I during the SR TY realingment in CARM NULL (transition from -220 to -222). This is not hidden by noise of the signal as the noise is +/-1e-9 peak to peak, while in figure 3 the transient is 3e-9.
This is most likely due to the change in the notch of the violin modes https://logbook.virgo-gw.eu/virgo/?r=67311 . We should return to the standard notch filters of the violin modes, undo the changes in the DCP pole frequency calculation done in CARM NULL 1F, and check if the SR alignment signals are recovered.
Due to WI issue an unlock occurred, the top stage guardian opened.
Inspecting the data (fig.1), we noticed data corrupted on the corrections signals.
ITF found in Science mode.
At 13:31 UTC ITF in Commissioning mode: the commissioning team worked all the day on the TCS/ISC tuning.
We were able to reach LN3 by the end of the shift using a new SR trick (instructions have been left for the next operator); locking in progress....
Note: According to Michal, in case of locking issues, leave the ITF in Troubleshooting mode with locked arms
SUSP
At 19:00 UTC WI ID opened by the guardian; loops closed by Manuel and Ettore.
Today we have connected the WEB loudspeaker too.
Now it's ready to work: smart_PDU socket 3, volume set at max, value of the amplitude parameter in the ini.file should be the same as NEB (Amp= 0.1)
Today, I found the ITF unlocked. During the locking acquisition, four locks were unsuccessful because of an unrequested PRWI, as suggested by D. Bersanetti (entry 67265). I stopped and restarted the CALI node from the VPM, and the lock was restored on the first attempt. We continue to experience locking problems, with some unlocks occurring at the levels of CARM_NULL_3F and REDUCING_CARM_OFFSET. Therefore, I contacted the TCS on-call, I. Nardecchia, to check the TCS power levels. P. Spinicelli and M. Pinto worked on recovering the ITF lock.
Another potential issue could be the ongoing microseismic activity caused by earthquakes in Alaska. I. Nardecchia found the WI CH a bit high, so she decreased the value by 12%. We experienced several unlocks while trying to reach CARM_NULL_3F. At 11:32 UTC, the ITF unlocked at ACQUIRE_LOW_NOISE_3, and DET_MAIN got stuck, so I requested an initialization of DET_MAIN to restart the locking process. 12:20 UTC ITF back in SCIENCE.
Sub-system reportsISYS
8:05 UTC P. Spinicelli changed the temperature setpoint of the Neovan head chiller from 16 to 15.5
ITF found in DOWN with EARTHQUAKE mode, unable to maintain ARMS_LOCK longer than minutes, then seconds due to strong earthquake at 20:37UTC: Location 54.549°N 160.472°W, Depth 20.1 km, Magnitude 7.3 (source: USGS).
Guard tour (UTC)
22:31 -> 23:08
00:59 -> 01:36
03:04 -> 03:39
DAQ
Still experiencing temporary data losses? see BNS range and gray DMS flags (fig.2)
DET
SDB2_B1p_QD1 and QD2 Vbias rearmed and Shutter opened at 22:40 and 23:05UTC.
The change in the DARM line phase due to the change in violin mode notch filters may have changed the demodulation phase for the the SDB1/OMC and SR alignment signals which are based on the demodulation of the 491.3Hz DARM line. For the moment it is not easy to say if it is the case or not, as the signals have a much higher noise due to the high amplitude of the violin modes.
Figure 1 shows a lock acquisition from a few days ago, when one can see the SDB1 TY misalignment by 10urad as the bench follows changes due to the SR misalignment. One can see a transient in the I quadrature (but not the Q) of SDB1_B1_DARM_TY, as the loop tries to follow. And one can see that ASC_SR_TY_DCP_HF_phi_B1_I acquires an offset, as SR is misaligned.
Figure 2 in the successful lock acquisition of today these signals are much more noisy, by about a factor 10, so these changes are not visible.
It may be the case that there is no issue, as SDB1/OMC looks at the magnitude of the line, which doesn't depend on the phase. And SR looks as the phase of the line, which acquires a static change, which is then removed by demodulation at the SR TX and TY line frequencies. If there is an issue, it is not too large, as both loops seem to work well enough to keep the interferometer aligned.
Once we reached CARM NULL 1f, we noticed that the DCP monitor was measuring 40Hz. We knew that the usual values are between 380 and 400Hz, and even if this probe is not used until LN3, at that stage it is used to "misalign" the SR, in particular we misalign it until the DCP reaches 175Hz. However, with the DCP monitor pointing 40Hz, the SR alignment loop wasn't working properly.
So we took a measurement of the OLTF of DARM while in CARM NULL 1f (09.13.38 UTC, 120s) and we adjusted the calibration factor accordingly in the ini file (from 32 to 275). Then we adjusted also the calibration in LN2 based on the same measurement (since there are no changes in the optical configuration in between), going from 148 to 1468. Finally we also compensated the calibration in LN3, and we made a last measurement to make sure that the misalinged position was indeed around 175Hz as requested (10.28.41 UTC, 120s). The range seemed recovered so we let the interferometer in this configuration.
ITF found in Troubleshooting mode.
The ITF kept unlocking at various steps; at around 6:00 UTC the commissioning team started to investigate the locking issues.
At around 7:00, triggered by a red flag on the DMS, I noted a decrease in power for the WI CO2 laser. I contacted Ilaria who adjusted the power; after waiting for the thermal transient the ITF was able to reach CARM_NULL_1F. We asked to go in LOW_NOISE_3 but the the commissioning team discovered a problem in the loop to misalign the PR.
After having fixed this issue the ITF reached LN3 and Science mode was set 10:39 UTC.
Yesterday we modified the notch fitler to face the reintroduction of noise at the WE violin modes frequencies. In order to improve the response we relaxed the Q ratio of the pole/sero structures. (fig.1,2)
The results was to loose an amount of phase at the DARM HF line frequency (491 Hz), see fig.3, and at the UGF of DARM (fig.4).
The results didn't affect the performance of the loop itself, but as a drowback this morning we had to retune the monitor of the DCP, which is based the loop for the alignment of SR.
A note for the future. The B1p galvo loops opening systematically during the lock acquisition usually means that SR is strongly misaligned, which puch offsets into the SDB1 alignment, and as a result the beam is far from the middle of the B1p quadrants on SDB2, out of the actuation range of the galvo. The solution for that is to realign SR, normally no action is actually needed on the quadrants or the SDB1 alignment. This was the case in the past three occurrence that I can remember in the last 12 months.
ITF found at CARM_NULL_1F in TROUBLESHOOTING mode waiting for Violin modes to subside. PSTAB loop still open.
Unlocks due to IMC unlock (UTC):
Attempted to lock in LN3 at 02:20UTC: LN2 achieved at 02:30UTC, unlocked at 02:31UTC due to Diffp oscillation (pdf 1). Automation reached LOCKING_CARM_NULL_3F before unlocking twice in the same way at 02:41 and 02:51UTC with SDB2_B1p_QD1 horizontal and vertical loops open. Unlocked in LOCKED_CARM_MC_IR at 03:04UTC with B1p_QD1 horizontal loop open. Then systematically in LOCKING_CARM_MC_IR at 03:12, 03:20 and 03:28UTC with both horizontal and vertical loops open (DMS plots in fig.2 and 3.)
Unlocked in LOCKING_CARM_NULL_3F at 03:37UTC and then in LOCKING_CARM_MC_IR at 03:45UTC. DET On-call (Was) notified as I cannot find a way to close B1p Quadrants loops beyond lock of CITF. (DMS plot in fig.4)
03:55 - 04:50UTC Attempted step by step lock acquisition twice up to LOCKED_CARM_MC_IR to isolate the issue. ITF keeps unlocking systematically (04:25 and 4:45UTC) beyond that point, so I parked it in LOCKED_ARMS_BEAT_DRMI_3F waiting for expert intervention.
05:19UTC After cross alignment of SR with assistance from Berni and Was, lock acquisition towards CARM_NULL_1F finally progressed up to CARM_NULL_3F, before unlocking again at 05:25UTC. Relocking in progress.
Guard tour (UTC)
-> 21:29
23:06 -> 23:50
01:15 -> 01:56
03:20 -> 03:56
DET
21:59-22:06UTC SDB2_B1p_QD1 and QD2 Vbias rearmed and Shutter opened during lock acquisition 3.
02:42-02:47UTC SDB2_B1p_QD2 Vbias rearmed and Shutter opened.
21:59-22:06UTC SDB2_B1p_QD1 and QD2 Vbias rearmed and Shutter opened.
04:39UTC SDB1 LC floating setpoints disabled by Was for Galvo quadrant intervention.
A note for the future. The B1p galvo loops opening systematically during the lock acquisition usually means that SR is strongly misaligned, which puch offsets into the SDB1 alignment, and as a result the beam is far from the middle of the B1p quadrants on SDB2, out of the actuation range of the galvo. The solution for that is to realign SR, normally no action is actually needed on the quadrants or the SDB1 alignment. This was the case in the past three occurrence that I can remember in the last 12 months.
After the realignment of the West Arm we tried the lock acquisition. Besides some issue with PSTAB, we unlocked due to the WE violin modes during the transition to LN2, fig.1.
We looked at the notches in the control filter and we noticed some miscentering of the notches wrt the excited modes. The DARM correction was substaining the noise at those frequencies so we sligthly modified the notch filter in order to limit the modes noise reintroduction (see Fig.2 for comparison)
Most likely the modes will naturally damp with their own tau (6 hours ca).
We leave the ITF in CARM null 1f, with the PSTAB loop open.
Yesterday we modified the notch fitler to face the reintroduction of noise at the WE violin modes frequencies. In order to improve the response we relaxed the Q ratio of the pole/sero structures. (fig.1,2)
The results was to loose an amount of phase at the DARM HF line frequency (491 Hz), see fig.3, and at the UGF of DARM (fig.4).
The results didn't affect the performance of the loop itself, but as a drowback this morning we had to retune the monitor of the DCP, which is based the loop for the alignment of SR.
Once we reached CARM NULL 1f, we noticed that the DCP monitor was measuring 40Hz. We knew that the usual values are between 380 and 400Hz, and even if this probe is not used until LN3, at that stage it is used to "misalign" the SR, in particular we misalign it until the DCP reaches 175Hz. However, with the DCP monitor pointing 40Hz, the SR alignment loop wasn't working properly.
So we took a measurement of the OLTF of DARM while in CARM NULL 1f (09.13.38 UTC, 120s) and we adjusted the calibration factor accordingly in the ini file (from 32 to 275). Then we adjusted also the calibration in LN2 based on the same measurement (since there are no changes in the optical configuration in between), going from 148 to 1468. Finally we also compensated the calibration in LN3, and we made a last measurement to make sure that the misalinged position was indeed around 175Hz as requested (10.28.41 UTC, 120s). The range seemed recovered so we let the interferometer in this configuration.
The change in the DARM line phase due to the change in violin mode notch filters may have changed the demodulation phase for the the SDB1/OMC and SR alignment signals which are based on the demodulation of the 491.3Hz DARM line. For the moment it is not easy to say if it is the case or not, as the signals have a much higher noise due to the high amplitude of the violin modes.
Figure 1 shows a lock acquisition from a few days ago, when one can see the SDB1 TY misalignment by 10urad as the bench follows changes due to the SR misalignment. One can see a transient in the I quadrature (but not the Q) of SDB1_B1_DARM_TY, as the loop tries to follow. And one can see that ASC_SR_TY_DCP_HF_phi_B1_I acquires an offset, as SR is misaligned.
Figure 2 in the successful lock acquisition of today these signals are much more noisy, by about a factor 10, so these changes are not visible.
It may be the case that there is no issue, as SDB1/OMC looks at the magnitude of the line, which doesn't depend on the phase. And SR looks as the phase of the line, which acquires a static change, which is then removed by demodulation at the SR TX and TY line frequencies. If there is an issue, it is not too large, as both loops seem to work well enough to keep the interferometer aligned.
After the problems encountered few days ago with the Fmoderr process, today we rechecked both calibrations (MC and LNFS). We found out that the mechanical one was a bit underestimated and we corrected it with the new value (8.5e-9 --> 7e-9).
We tested twice the new value and everything seems to work correctly.
During the night we left the PSTAB open and no INJ unlocks were observed.
We optimized the alignment of the beam in the AOM before the PMC (which is the actuator for the PSTAB. The beam must be close to the edge, see photo1), looking at the transmission of the PMC while scanning and minimizing the misalignment mode 01. To be noticed that there are strange structures close to the 01 (photo 2). An improvement can be observed up to 10Hz (plot 3).
Another test we would like to perform is to lower the chiller temperature setpoint for the Neovan head from 16° to 15°, but we didn't do it this morning to decouple from the alignment.
