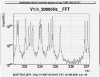
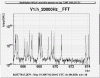
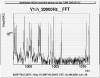
Violin modes are well evident in the Virgo spectrum (330-340Hz fundamental mode, see first attached figure, and multiples for the other modes). We expect to have 16 fundamental violin modes (4 mirrors X 4 wires), but if we look the second and the third attached figure we can count 22 or more lines. In effect each violin mode could be a doublet because the constrain (lower clamping) is asymmetric in the x and z directions and this could remove the mode degeneration. In the 4th attached picture a model of the violin frequency variation vs the wire temperature is reported (for the first 7 modes); taking in account the temperature stability inside the tower ad the 0.01Hz resolution of the line monitor tool, any frequency variation, induced by the temperature, should be detectable. The 5th figure, where all the violin modes are reported, seems to confirm this statement.

But few violin modes are showing some (small) sudden frequency variation: in the 6th and 7th figure some violin mode, represented by the black squares, shows  a jump (larger than the 0.01Hz of our resolution). The 8th figure show the same jump for the 2nd mode (660Hz). The red curve represents the frequency variation of the mysterious and huge bump at 750Hz. Some (but not all) abrute frequency variation of the bump seems to correspond to the jumps in the violin mode frequency. This could be due to the fact that the "strong" unlocks that are changing the violin frequenciy are also affecting the unknown origin of the mysterious 750Hz bump. If we will be able to assign all the violin modes to the corresponding mirrors, maybe we will be able to locate the source of the 750Hz bump. Some commissioning activity should be addressed to this direction.

By the way, the jump in frequency of the violin mode is about 30mHz that corresponds to a variation of the wire tension of about 10mN (and the tension is about 50N).